Prepare as per the the syllabus
Session Ending Examination
SUBJECT | Physics | 1 Periodic Test: 2022-23 | CLASS | XI |
TIME | 90 MIN |
| MAX.MARK | 40 |
INSTRUCTIONS: |
All questions are compulsory. Q. No. 1–4 are MCQ , carrying 1 mark each. Q. No. 5 is case study based, carrying 1x4=4 marks Q. No. 6 - 9 are very short answer questions, carrying 1 mark each. Q. No.10 is an Assertion Reasoning Question of 1x3=3 marks. Q. No.11 -14 are short answer questions, carrying 2 marks each. Q. No.15 -18 are long answer questions, carrying 3 marks each. Q. No .19 is a very long answer type question of 5 marks.
|
Q.1 | The number of significant figures in 0.010200 m is: A. 2 B. 3 C. 4 D. 5 | 1 |
Q.2 | The symbol of S. I. unit of luminous intensity is: A. lm B. Li C. Cd D. cd | 1 |
Q.3 | Which of the following physical quantities has the dimensions of [ML-1T-2] A. pressure B. work C. power D. momentum | 1 |
Q.4 | A particle moves along the x axis from xi to xf . Of the following values of the initial and final coordinates, which one results in a negative displacement? A. xi = 5m, xf = 4m B. xi = −4m, xf = 1m C. xi = −4m, xf = 2m D. xi = −4m, xf = −2m | 1 |
Q.5 | Two vectors A and B are said to be equal if, and only if, they have the same magnitude and the same direction. Multiplying a vector A with a positive number λ gives a vector whose magnitude is changed by the factor λ but the direction is the same as that of A. To find the sum of vectors A + B, we place vector B so that its tail is at the head of the vector A. Then, we join the tail of A to the head of B. This line OQ represents a vector R, that is, the sum of the vectors A and B. 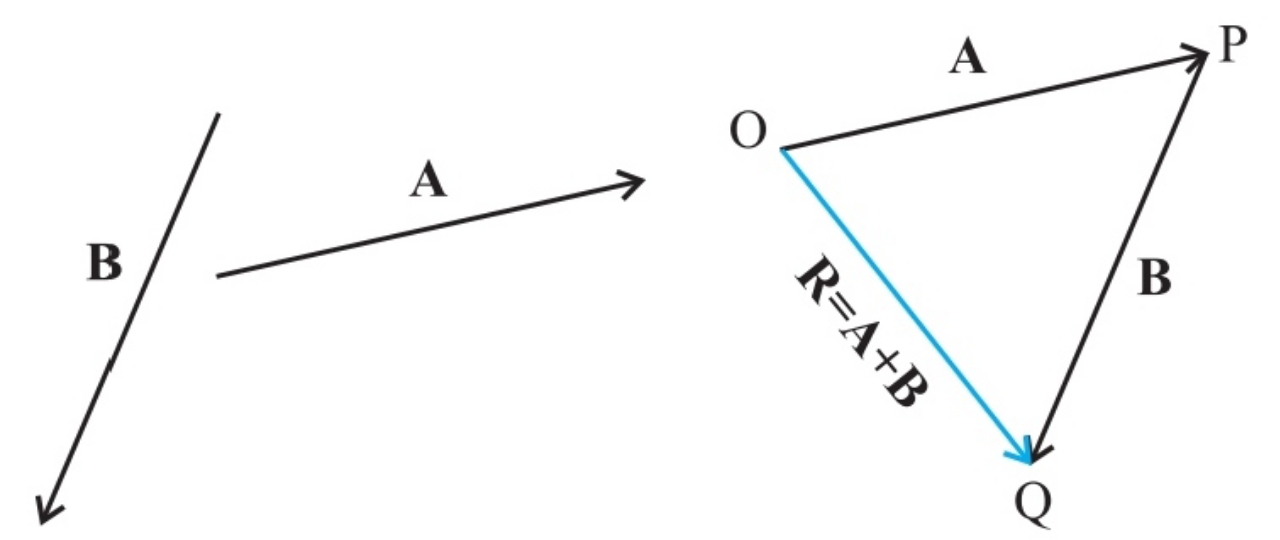
We define the difference of two vectors A and B as the sum of two vectors A and –B. A unit vector is a vector of unit magnitude and points in a particular direction. (i) a unit vector along the sum of unit vectors ( i + j ) along x and y axes is i+j (i+j).√2 (i+j)/√2 1
(ii) the direction of ( vector A + vector B) is Same as vector A - vector B Opposite to (vector A - vector B) Opposite to (vector B - vector A) None of these
(iii) if vector A=( 2 i + 3j ) and vector B = (2 i - 6j ), then (vector A + vector B) has magnitude 1 9 5 4
(iv) select the correct statement A unit vector has a particular dimension. A unit vector has a particular direction. The product of a vector with its magnitude gives a unit vector along it. None of these.
| 1x4 |
Q.6 | 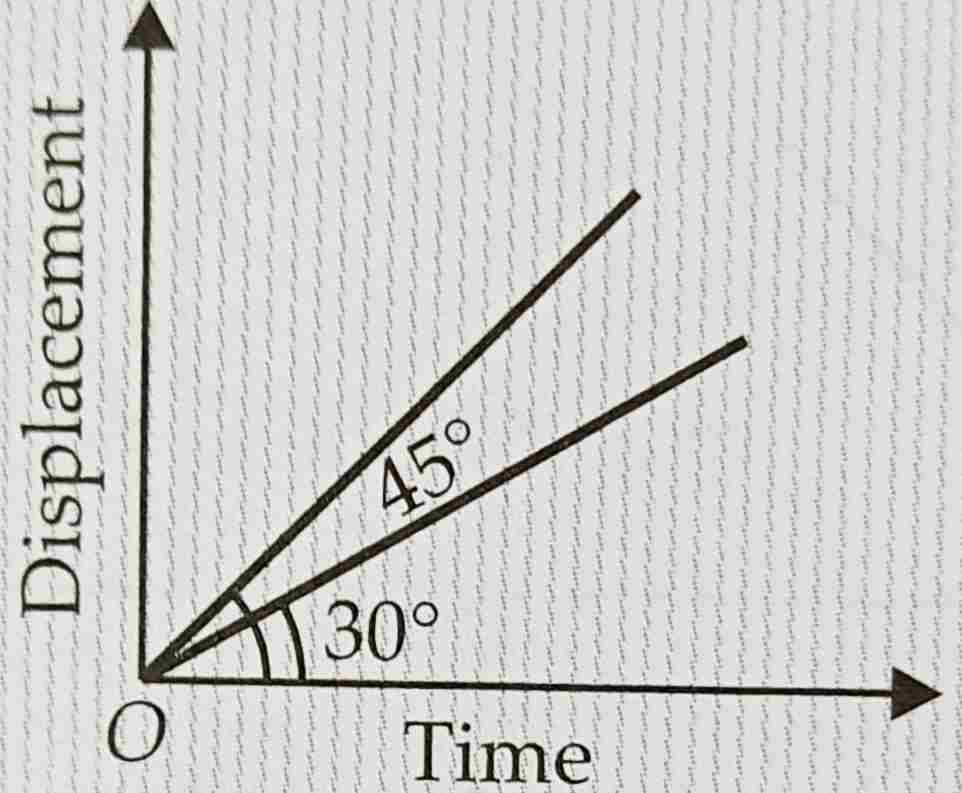
The displacement time graphs of two moving particles make angles of 30 degree and 45 degree with the time axis. The ratio of their velocities is √3:2 1:1 1:2 1:√3
| 1 |
Q.7 | A ball is dropped from the top of a building 100 metre high. At the same instant another ball is thrown upwards with a velocity of 40 m per second from the bottom of the building. The two balls will meet after 2 s 2.5 s 3 s 5 s
| 1 |
Q.8 | 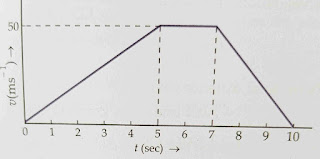
The velocity time graph of a body moving in a straight line is shown. The total distance travelled by the body is 200 m 300 m 400 m 600 m
| 1 |
Q.9 | What is a displacement vector? | 1 |
Q.10 | Directions: In the following questions, a statement of a assertion (A) is followed by a statement of reason (R ). Mark the correct choice as: if both assertion and reason are true and reason is the correct explanation of the assertion. If both assertion and reason are true but reason is not the correct explanation of the assertion. If the assertion is true but the reason is false. If both assertion and reason are false.
(i) Assertion: A body can have acceleration even if it's velocity is zero at that instant of time. Reason: The body will be momentarily at rest when it reverses its direction of motion. (ii)Assertion: When a body is dropped or thrown horizontally from the same height it would reach the ground at the same time. Reason: Horizontal velocity has no effect on the vertical motion. (iii)Assertion: Displacement of a body may be zero when distance travelled by it is not zero. Reason: The displacement is the longer distance between initial and final positions. | 1x3 |
Q.11 | Check whether the relation mv2 = mgh is dimensionally correct or not. | 2 |
Q.12 | Define instantaneous velocity. Is the magnitude of instantaneous velocity different from the magnitude of instantaneous speed? | 2 |
Q.13 | convert the unit: 6.67 × 10–11 N m2 (kg)–2 = ........... (cm)3 s–2 g–1. | 2 |
Q.14 | Write the dimensional formula of these physical quantities: electric potential V, universal constant of gravitation G | 2 |
Q.15 | Draw these graphs (curves): v-t graph for uniformly accelerated motion x-t graph for uniformly accelerated motion An object is thrown vertically into the air. Draw a graph which represents the velocity (v) of the object as a function of the time (t)? The positive direction is taken to be upward.
| 3 |
Q.16 | A particle starts from the origin at t = 0 s with a velocity of 10.0 j m/s and moves in the x-y plane with a constant acceleration of (8.0 i + 2.0 j) m.s-2. (a) At what time is the x- coordinate of the particle 16 m? What is the y-coordinate of the particle at that time? (b) What is the speed of the particle at the time ? OR A cyclist is riding at a speed of 18 km/h. As he approaches a circular turn on the road of radius 100 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn? | 3 |
Q.17 | Consider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using method of dimensions. | 3 |
Q.18 | A car is moving along a straight line, say OP in Figure. It moves from O to P in 18 s and returns from P to Q in 6.0 s. What are the average velocity and average speed of the car in the whole journey, i.e. going from O to P and back to Q ? | 3 |
Q.19 | Find a mathematical expression for the path of a projectile which is thrown at an angle θ above horizontal. Show that the projection angle θ for a projectile launched from the origin is given by θ = tan-1(4H/R) Here the symbol H = maximum height attained by the projectile and R = the range of the projectile. OR Explain with the help of vectors how a uniform circular motion is a kind of accelerated motion. Hence, find the expression for centripetal acceleration. An insect trapped in a circular groove of radius 15 cm, moves along the groove steadily and completes 7 revolutions in 100 s. (a) What is the angular speed, and (b) the linear speed.
| 5 |




I PERIODICAL TEST 2019-20
CLASS XI SUBJECT PHYSICS
TIME: 90 MIN MM: 50
| An object, tied to a string, moves in a circle at constant speed on a horizontal surface as shown. The direction of the displacement of this object, as it travels from W to X is:
| 1 |
| Explanation of photoelectric effect and Theory of relativity was given by: Archimedes Albert Einstein Isaac Newton W.K. Roentgen
| 1 |
| Electric generator works on the scientific principle of: Superconductivity Conversion of gravitational potential energy into electrical energy Motion of charged particles in electromagnetic fields Faraday’s laws of electromagnetic induction
| 1 |
| A stone is thrown horizontally and follows the path XYZ shown. The direction of the acceleration of the stone at point Y is:
| 1 |
| A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion: (a) y = a sin 2π t/T (b) y = a sin vt (c) y = (a/T) sin t/a (d) y = (a 2) (sin 2πt / T + cos 2πt / T ) (a = maximum displacement of the particle, v = speed of the particle. T = time-period of motion). Select the correct formula on dimensional grounds. | 1 |
| The value of 1.513 + 27.3 = A. 28.8 B. 28.9 C. 28.81 D. 28.813 | 1 |
| The number of significant figures in 0.00150 is: A. 2 B. 3 C. 4 D. 5 | 1 |
| A nanosecond is: A. 10-6 s B. 10−9 s C. 10−10 s D. 10−12 s | 1 |
| The unit for area is a derived unit because: A. an area has no thickness; hence no physical standard can be built B. we live in a three (not a two) dimensional world C. it is impossible to express square feet in terms of meters D. area can be expressed in terms of square meters | 1 |
| The vectors a, b, and c are related by c = b − a. Which diagram below illustrates this relationship?
| 1 |
| A particle moves along the x axis from xi to xf . Of the following values of the initial and final coordinates, which one results in a negative displacement? A. xi = 4m, xf = 6m B. xi = −4m, xf = −8m C. xi = −4m, xf = 2m D. xi = −4m, xf = −2m | 1 |
|
Which of the above position versus time graphs represents the motion of an object whose speed is increasing? | 1 |
| A car starts from point P, goes 50 km in a straight line to point B, immediately turns around, and returns to P. The time for this round trip is 2 hours. the average speed of the car for this round trip is: A. 0 B. 50 km/h C. 100 km/h D. 200 km/h | 1 |
| An object is thrown vertically into the air. Which of the following graphs represents the velocity (v) of the object as a function of the time (t)? The positive direction is taken to be upward.
| 1 |
| The diagram represents the straight line motion of a car. Which of the following statements is true?
A. The car accelerates, stops, and reverses B. The car accelerates at 6 m/s2 for the first 2 s C. The car returns to its starting point when t = 9 s D. The car decelerates at 12 m/s2 for the last 4 s | 1 |
| Explain any two sources of systematic errors. | 2 |
| Convert Nm2 (kg)–2 = ......... (cm)3 s–2 g–1. | 2 |
| Define : Average speed, instantaneous velocity | 2 |
| A girl wishes to swim across a river to a point directly opposite as shown. She can swim at 2m/s in still water and the river is flowing at 1m/s. At what angle θ with respect to the line joining the starting and finishing points should she swim?
| 2 |
| A boy on the edge of a vertical cliff 20m high throws a stone horizontally outward with a speed of 25m/s. at what horizontal distance from the foot of the cliff it strikes the ground? Use g = 10m/s2. | 2 |
| Over a short interval, starting at time t = 0, the coordinate of an automobile in meters is given by x(t) = 27t − 4.0t3, where t is in seconds. Find the magnitudes of the initial (at t = 0) velocity and acceleration of the auto. | 3 |
| The velocity v of sound in air may depend on atmospheric pressure P and density of air D. write the dimensional formula for v, P and D and find a relation for v in terms of P and D. | 3 |
| Draw vectors and find expression for centripetal acceleration during uniform circular motion. | 3 |
| Explain the method of parallax to find the distance of a nearby planet. OR Define 1 A. U. and use it to find the value of 1 parsec. | 3 |
| Name the fundamental forces in nature. Write any two properties of the strongest force. | 3 |
| For an oblique projectile, find an expression for time of flight T, maximum height H and the range R of projectile. | 5 |
| Define uniformly accelerated motion and derive following equations of motion using graph: v = u + a.∆t, ∆x = u.∆t + a(∆t)2/2 | 5 |
I PERIODIC TEST SESSION 2017-18
CLASS XI SUBJECT PHYSICS
TIME 90 MIN MM 50
| What is the S.I. unit of luminous intensity? | 1 |
| A stone thrown vertically upward fall on ground after sometime. Show a curve for the Variation of its velocity with time. | 1 |
| What is the order of magnitude of 0.00701m? | 1 |
| Fill in the blanks by suitable conversion of units: 1 kg m2s–2 = ....g cm2 s–2 | 2 |
| Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval (1, 2 or 3) is the average acceleration greatest in magnitude? In which interval average speed in minimum?
| 2 |
| The energy E of a particle is given in terms of time t by the equation E = at + b/(t+c). Find the dimensions of ‘a’ and ‘c’. | 2 |
| What digits are known as significant digits/figures?5.74 g of a substance occupies 1.2 cm3. Round off the result and express its density by keeping the significant figures in view. (Given that 5.74/1.2 = 4.7833333) | 2 |
| Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h–1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service on the road? | 3 |
| What is parallax? Explain the method of parallax to find the diameter of moon | 3 |
| Write any three properties of electromagnetic force and nuclear force. | 3 |
| What are Systematic errors? Name their different sources. | 3 |
| We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 1.55 s, 1.50 s, 1.40 s, 1.70s and 1.75 s. Calculate the absolute errors and relative error. | 3 |
| Speed of sound in air may depend on the density d and pressure P of air. Find a relation for the speed using the method of dimensions. | 3 |
| A player throws a ball upwards with an initial speed of 29.4 m s–1.(a) What is the acceleration of the ball at the highest point of its motion?(b) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance). | 3 |
| Rain is falling vertically with a speed of 36 m s–1. Winds starts blowing after sometime with a speed of 12 m s–1 in east to west direction. Draw vector diagram and find the direction in which a boy waiting at a bus stop should hold his umbrella? | 3 |
| Derive the equations of motion ∆x = ut + at2/2 and v2 – u2 = 2a∆x by uv-graph method. | 5 |
| Define instantaneous velocity.Position time graph of a particle is show below. State whether the particle is moving with zero/positive or negative velocity?
 The position of an object moving along x-axis is given by x = a + bt2 where a = 6 m, b = 2 m s–2 and t is measured in seconds. What is its velocity at t = 2.0 s. What is the average velocity between t = 2.0 s and t = 4.0 s?
| 5 |
| Write the triangle law of vector addition. Define: unit vector, equal vectors. Explain how you would subtract a vector A from another given vector B. ………………. | 5 |
Unit Test (Retest): 2013
Duration: 90 min XI Physics M. Marks: 40
1 Define instantaneous velocity. 1M
2 name the weakest force of nature. 1M
3 name the scientist who is credited for the laws of electromagnetic induction. 1M
4 Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? 1M
5 Round off these values to three significant figures: 1M
2.745 b. 63.821 g
6 fill in the blanks:
a. 1 fermi = 1 f = ………..m
b. 1 angstrom = 1 Å = ………..m
c. 1 astronomical unit = 1 AU (average distance of the Sun from the Earth) = …………………m
d. 1 light year = ……………m. 2M
7 Which of the following is the most precise device for measuring length :
(a) a vernier callipers with 20 divisions on the sliding scale.
(b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale 2M
8 State the number of significant figures in the following :
(a) 0.0070 m2
(b) 2.64 × 1024 kg 2M
6 differentiate between base units and derived units. 2M
9 explain systematic error in measurement. 3m
10 We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 2.63 s, 2.56 s, 2.42 s, 2.71s and 2.80 s. Calculate the absolute errors and relative error 3M
11 explain method of parallax to measure the diameter of Moon. 3M
12 A physical quantity P is related to four observables a, b, c and d as follows :
P=a3b2/( c d)1/2
The percentage errors of measurement in a, b, c and d are 1%, 2%, 4% and 2%,
respectively. What is the percentage error in the quantity P ? 3M
13 A car is moving along a straight line, say OP in Fig. It moves from O to P in 18 s and returns from P to Q in 6.0 s. What are the average velocity and average speed of the car in going from O to P and back to Q ? 3M
14 Two trains A and B of length 400 m each are moving on two parallel tracks with a
Uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of
B decides to overtake A and accelerates by 1 m s–2. If after 50 s, the guard of B just
brushes past the driver of A, what was the original distance between them ? 3M
15 Let us consider an equation m v2 = m g h
where m is the mass of the body, v its velocity, g is the acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct.
16 Consider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using method of dimensions. 5M
17 derive equations of motion for uniformly accelerated motion of an object. 5M






















Comments
Post a Comment